【結論】バーコードは数学的なルールで正確に読み取られている
バーコードは、見た目こそ黒と白の線が並んでいるだけに見えますが、
実際には数学的なルールと計算によって情報が正確に管理されています。
線の太さや並びには明確な意味があり、読み取り機はそれを数値として解析しています。
人間が目で見て数字を読むのではなく、
数として処理できる形に変換されていることが、
バーコードが高速かつ正確に読み取れる最大の理由です。
この仕組みを理解すると、なぜバーコードが読み間違えにくいのか、
なぜエラーが検出されるのかが自然と見えてきます。
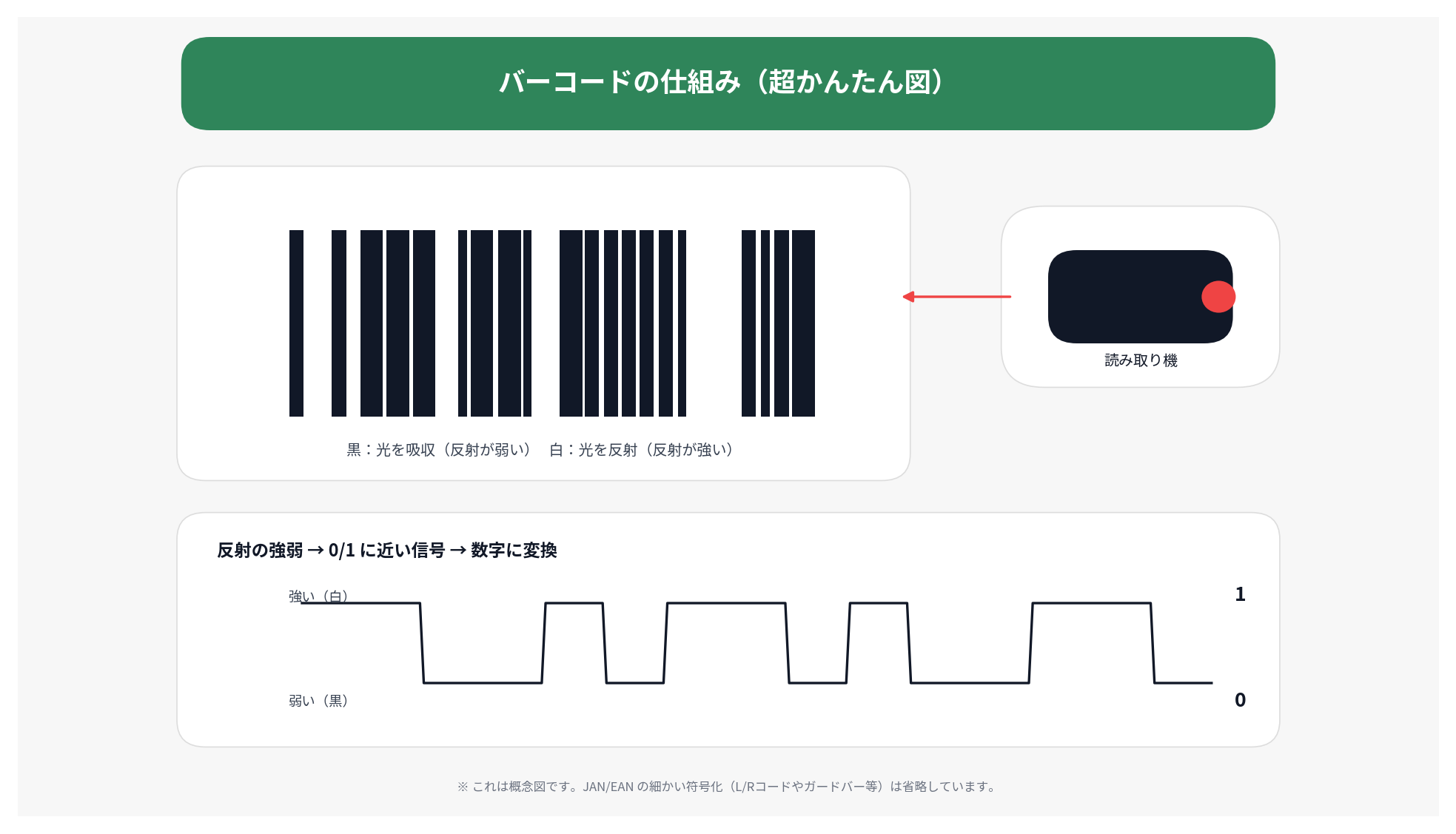
※実際のバーコードでは、黒白の「幅の比率」をもとに数字が符号化されています。本図は「光の反射を数値として処理する」という原理を分かりやすく示した概念図です。
バーコードの仕組みを理解するための基本知識
バーコードを数学的に理解するためには、
まず「バーコードとは何か」という基本から整理する必要があります。
多くの人は、バーコードを単なる商品識別用の印刷物だと考えがちですが、
実際には情報を機械に正確に伝えるために設計された記号体系です。
バーコードは、人間が目で数字を読み取ることを目的としていません。
あくまで、読み取り機が光を照射し、
その反射の違いを数値として取得し、
内部で計算処理することを前提に作られています。
つまり、バーコードとは「視覚的な模様」ではなく、
数として扱える形に変換された情報だと考えると理解しやすくなります。
この前提を押さえておくことで、
なぜ数学がバーコードの仕組みに深く関わっているのかが見えてきます。
バーコードとは何か?黒と白の線の正体
バーコードに描かれている黒い線と白い空白は、
見た目こそ単純ですが、明確な役割を持っています。
これらは単なるデザインではなく、
光の反射量の違いを利用した情報表現です。
黒い部分は光をほとんど反射せず、
白い部分は強く反射します。
読み取り機はレーザーやLEDの光をバーコードに当て、
返ってくる光の強さを連続的に測定します。
この反射光の変化は、
強い・弱いという感覚的なものではなく、
数値データとして記録されます。
そのため、バーコードは画像として処理されるのではなく、
時間ごとの数値の変化として扱われます。
この仕組みによって、
バーコードは「黒と白の模様」ではなく、
数値の並びとして読み取られるようになります。
ここが、人間の視覚による認識と、
機械による読み取りの決定的な違いです。
なぜ線の太さや間隔で数字が表せるのか
バーコードでは、線の「太い・細い」や、
線と線の間隔があらかじめ定められたルールに従っています。
ランダムに引かれているわけではなく、
すべてが数学的な規則に基づいて配置されています。
たとえばJANコードでは、
一定の幅を最小単位とし、
その単位が何個分連続しているかによって数字を表現します。
この方法により、
線の組み合わせを数として扱うことが可能になります。
この考え方は、
モールス信号やデジタル通信の仕組みとよく似ています。
短い信号と長い信号の組み合わせで意味を伝えるように、
バーコードでも幅の違いを使って情報を伝えています。
重要なのは、
絶対的な長さではなく比率で判断している点です。
多少印刷が大きくなったり小さくなったりしても、
基準となる幅との比が保たれていれば、
正しく読み取れるように設計されています。
バーコードは情報をどこまで表現できるのか
一般的なJANコードでは、
商品を識別するための数字が表現されています。
その内訳は、
事業者を示すコード、商品を示すコード、
そしてチェックデジットに分かれています。
一見すると情報量は少なく感じるかもしれませんが、
バーコードの目的は、
大量の情報を詰め込むことではありません。
商品を一意に識別できる最低限の情報を、
高速かつ正確に伝えることに特化しています。
この割り切りがあるからこそ、
レジや物流の現場では、
一瞬で商品情報を処理することが可能になります。
もしバーコードに過剰な情報を持たせてしまうと、
読み取り速度や信頼性が大きく低下してしまいます。
バーコードは、
「何でも表現できる万能な仕組み」ではなく、
役割を限定した数学的に合理的な情報表現だと理解すると、
その設計思想がより明確になります。
バーコードと数学の関係
バーコードの仕組みは、
実は中学校レベルの数学の考え方と深く結びついています。
特別な数式や難解な理論が使われているわけではなく、
数の並び・規則性・単純な計算といった、
誰もが一度は学んだ要素の組み合わせで成り立っています。
そのため、バーコードの仕組みは、
「理系向けの高度技術」というよりも、
基礎数学を実用レベルまで落とし込んだ仕組み
と考えると理解しやすくなります。
数学が苦手だと感じている人でも、
考え方自体は決して難しいものではありません。
ここでは、バーコードがどのように数字として扱われ、
どんな数学的発想によって安定した読み取りが実現しているのかを、
順番に整理していきます。
バーコードは数字をどのように数値化しているか
読み取り機は、バーコードを写真や画像として処理しているわけではありません。
バーコードに光を当て、
返ってくる反射光の強さの変化を時間の流れとして記録し、
それを数値データに変換しています。
具体的には、
光が強く返る部分と弱く返る部分の切り替わりを検出し、
その切り替わりの間隔を測定します。
この間隔が、
「どれくらいの幅の線なのか」
「どれくらいの空白なのか」
を判断する材料になります。
読み取り機は、最終的にはバーコードを
画像ではなく数値として処理します。
レーザー方式やカメラ方式など取得方法には違いがありますが、
いずれの場合も、反射や明るさの変化を数値化し、
計算によって判定する点は共通しています。
この処理によって、
バーコードは単なる模様ではなく、
幅の長さが並んだ数の列として扱われます。
つまり、読み取り機の内部では、
バーコードは視覚情報ではなく、
数列データとして処理されているのです。
この数列が、
あらかじめ決められた規則と一致するかどうかを確認しながら、
数字へと変換されます。
この「規則に照らし合わせて判定する」という考え方も、
数学の基本的な発想のひとつです。
2進数の考え方とバーコードの共通点
バーコードは、コンピューターで使われる
厳密な2進数そのものではありませんが、
考え方は非常に近いものがあります。
黒い線と白い空白、
反射が弱い部分と強い部分というように、
状態が大きく2つに分かれる仕組みを利用して、
情報を区別している点が共通しています。
これは、0と1だけで情報を扱う2進数と同じ発想です。
状態をあいまいにせず、
はっきり分けることで、
誤認識を減らすことができます。
もし、黒と白の区別があいまいだった場合、
少しの汚れや印刷のかすれで、
正しく読み取れなくなってしまいます。
しかし、二択に近い状態で判定することで、
多少の誤差があっても、
正しい側に分類しやすくなるのです。
このように、
バーコードは「単純な状態の組み合わせ」で
情報を表現することで、
高い信頼性を実現しています。
これも数学的な単純化の考え方が
実用に活かされている例だと言えます。
線と空白を数として扱う数学的発想
バーコードの読み取りで特に重要なのが、
線と空白の相対的な比率です。
バーコードでは、
線の絶対的な長さそのものよりも、
基準となる幅に対して何倍かという関係が重視されます。
たとえば、
基準となる幅を1としたときに、
2倍の幅なのか、3倍の幅なのかを判断することで、
数字を区別しています。
この考え方は、
数学で学ぶ比例や比の考え方とそのまま一致します。
この仕組みのおかげで、
バーコードは拡大・縮小されても正しく読み取れます。
印刷サイズが多少違っていても、
比率が保たれていれば、
同じ数字として認識できるのです。
もし絶対的な長さだけで判断していた場合、
印刷誤差や読み取り距離の違いによって、
すぐにエラーが発生してしまいます。
相対的な関係で判断するという数学的発想が、
現実の環境に強い仕組みを支えています。
このように、
バーコードは数学の基本概念である
数・比・規則を組み合わせることで、
高速かつ安定した読み取りを可能にしています。
数学が実社会でどのように使われているかを知るうえでも、
非常に分かりやすい例と言えるでしょう。
JANコードに使われている数学的ルール
日本で最も身近なバーコードであるJANコードには、
見た目以上にしっかりとした数学的ルールが組み込まれています。
ただ数字を並べているだけではなく、
読み取りミスを防ぐための計算が前提として設計されています。
その代表的な仕組みが、
バーコードの末尾に配置されている
チェックデジットです。
この1桁の数字があることで、
バーコードは高い信頼性を保っています。
JANコードの構成と数字の並び方
JANコードは、大きく分けて
3つの要素から構成されています。
最初の部分は、
商品を製造または販売している事業者を識別するための数字です。
この部分によって、
どの会社が管理している商品なのかが分かります。
次に続く数字は、
その事業者が管理する商品の種類を表す番号です。
同じ会社の商品であっても、
商品ごとに異なる番号が割り当てられています。
そして最後の1桁が、
チェックデジットです。
この数字は商品を表すための情報ではなく、
あくまで「正しく読み取れたかどうか」を確認するために存在しています。
このように、JANコードの数字は、
左から順番に意味を持って並んでおり、
単なる連番やランダムな数字ではありません。
構造を理解すると、
バーコードが論理的に設計されていることが分かります。
チェックデジットとは何か
チェックデジットとは、
読み取りミスや入力ミスを検出するための確認用の数字です。
人が数字を目で見て入力した場合や、
機械がバーコードを読み取った場合でも、
誤りが発生する可能性はゼロではありません。
そこでJANコードでは、
末尾にチェックデジットを付けることで、
「この数字の並びは正しいかどうか」を
計算によって判定できるようにしています。
もし途中の数字が1桁でも間違っていれば、
計算結果が合わなくなり、
エラーとして検出される仕組みです。
重要なのは、
チェックデジットは「正解を当てるための数字」ではなく、
「間違いを見つけるための数字」だという点です。
この考え方は、
数学における誤り検出の発想そのものです。
そのため、チェックデジットが一致しない場合、
バーコードは読み取れなかったり、
システム上でエラーとして扱われます。
これにより、
誤った商品情報が登録されるリスクを大きく減らしています。
チェックデジットの計算方法を数学的に解説
JANコードのチェックデジットは、
単純な足し算と掛け算を組み合わせた計算によって決まります。
難しい数式は使われておらず、
基本的な計算ルールだけで成り立っています。
具体的には、
バーコードの各桁の数字に対して、
あらかじめ決められた「重み」を掛け、
その結果をすべて足し合わせます。
この合計値が、
特定の数で割り切れるように、
最後のチェックデジットが調整されます。
逆に言えば、
途中の数字が1つでも変わると、
合計値が変わり、
割り切れなくなります。
この仕組みによって、
1桁の読み間違いや、
数字の入れ替わりといったミスが、
非常に高い確率で検出されます。
すべての誤りを完全に防げるわけではありませんが、
現実的なミスの多くを効率よく見つけられる
という点で、
チェックデジットは非常に優れた仕組みです。
複雑な計算を使わず、
シンプルな数学のルールだけで、
ここまで高い信頼性を実現している点は、
JANコードの設計がいかに実用的かを示しています。

バーコードが読み間違えにくい理由
バーコードは、
人間が目で数字を読み取る場合と比べて、
はるかに高い精度で情報を扱うことができます。
この差は、性能の良い機械を使っているからというだけではありません。
最大の理由は、
バーコードの設計そのものに
数学的な誤り検出の仕組みが組み込まれている点にあります。
あらかじめ「間違いが起きる前提」で作られているため、
読み取り時に異常を見つけやすくなっているのです。
数学的な誤り検出の仕組み
バーコードが読み間違えにくい最大の理由は、
チェックデジットによる計算による確認が行われていることです。
読み取り機は、バーコードを読み取ったあと、
必ず内部で計算を行い、
その数字の並びが正しいかどうかを検証します。
もし読み取った数字が、
設計されたルールと一致しなければ、
その時点でエラーとして扱われます。
このため、
「なんとなくそれっぽい数字」が
そのまま通ってしまうことはほとんどありません。
人間の場合は、
多少違和感があっても
「たぶん合っているだろう」
と判断してしまうことがありますが、
機械は計算結果が合わなければ
必ず不正と判断します。
この違いが、
読み取り精度の大きな差につながっています。
1桁間違ってもエラーになる理由
JANコードでは、
各桁の数字に異なる重みを掛けて計算する仕組みが使われています。
このため、
途中の数字が1桁変わるだけでも、
合計値が大きく変化します。
仮に数字を1つ読み間違えた場合でも、
その影響は単純な足し引きにとどまらず、
計算全体に波及します。
結果として、
チェックデジットとの整合性が取れなくなり、
エラーとして検出されます。
「たまたま間違っても計算が合ってしまう」
というケースは、
理論上はゼロではありませんが、
現実的には極めて起こりにくい
ように設計されています。
このように、
1桁のミスであっても見逃されにくい点が、
バーコードの信頼性を支える重要な要素です。
なぜ人間より機械の方が正確に読めるのか
人間が数字を読むときは、
どうしても感覚や経験に頼る部分があります。
文字がかすれていたり、
一部が見えにくかったりすると、
脳が自動的に補完して判断してしまいます。
一方、機械は
感覚ではなく数値でしか判断しません。
光の反射量、変化のタイミング、間隔といった
物理的な情報をそのまま数値化し、
決められたルールに当てはめて処理します。
そこには、
「たぶんこうだろう」
「前後の流れから考えて」
といった曖昧な判断が入り込む余地がありません。
この曖昧さの排除こそが、
人間よりも機械の方が
安定して正確にバーコードを読み取れる理由です。
数学的なルールに従って処理することで、
誰が使っても同じ結果が得られる仕組みが実現されています。
数学で理解するとトラブル対応が楽になる
バーコードの仕組みを数学的に理解していると、
トラブルが起きたときの対応が格段に楽になります。
これは知識自慢のためではなく、
原因を切り分ける視点が明確になるためです。
バーコードが読み取れない場面では、
「機械が壊れているのでは」
「印刷ミスでは」
と感覚的な推測が先に立ちがちですが、
数学的な仕組みを知っていれば、
問題を順序立てて考えることができます。
つまり、
どこで数のルールが崩れているか
を冷静に確認できるようになるのです。
感覚ではなく原因を切り分けられるようになる
バーコードの読み取りトラブルは、
大きく分けると
「光の読み取り段階」
「数値変換の段階」
「計算確認の段階」
のどこかで問題が起きています。
数学的な視点を持っていれば、
「反射は取れているか」
「線の幅が基準単位として認識されているか」
「チェックデジット計算で弾かれていないか」
と、順番に確認できます。
これは、
原因を一気に当てに行くのではなく、
論理的に潰していく
というアプローチです。
結果として、
無駄な再スキャンや、
不要な機器交換を減らすことにもつながります。
「とりあえず拭く」以外の判断ができる
バーコードが読めないとき、
最初に行われがちなのが
「汚れを拭く」
「角度を変える」
といった対処です。
もちろんこれらは有効ですが、
数学的な仕組みを知っていると、
それがなぜ有効なのかを説明できます。
たとえば、
拭く行為は単なる清掃ではなく、
「反射量の差を数値として安定させる」
という意味を持っています。
角度を変えるのも、
線と空白の境界が
読み取り単位として正しく検出されるようにするためです。
理由が分かっていれば、
状況に応じて
「拭くべきか」
「再印刷すべきか」
「手入力に切り替えるべきか」
を素早く判断できます。
バーコードが読み取れない原因も数学で説明できる
バーコードが読み取れない理由は、
決して曖昧なものではありません。
多くの場合、
数として扱えなくなった瞬間
が存在します。
数学の視点で見ると、
読み取りエラーは
「数の前提条件が崩れた状態」
だと考えることができます。
線や空白が基準単位として認識されない
バーコードは、
線と空白の幅を
「基準単位の何倍か」
として読み取っています。
しかし、
印刷がにじんでいたり、
曲面に貼られていたりすると、
この比率が崩れます。
すると読み取り機は、
「どこまでが1単位か」
を判断できなくなります。
これは、
数字で言えば
小数点の位置が分からなくなったような状態です。
数として成立しないため、
その後の計算にも進めません。
反射量の差が数値として区別できない
バーコードは、
黒と白の反射量の差を利用しています。
ところが、
汚れや光の映り込みがあると、
この差が小さくなります。
結果として、
「黒なのか白なのか」
という判定が曖昧になり、
数値化の段階でエラーが発生します。
数学的に言えば、
0と1の区別がつかなくなった状態であり、
その先の処理が成立しなくなります。
チェックデジット計算で弾かれている
見た目には正しく読み取れているように見えても、
最後のチェックデジット計算で
エラーになるケースもあります。
この場合、
読み取り機は
「数字としては取得できたが、
計算結果が合わない」
と判断しています。
これは、
入力された数列が
数学的に正しくない
と判断された状態です。
そのため、
システムはあえて処理を止め、
誤登録を防いでいます。
数で考えると対処法が明確になる
バーコードが読めない原因を
「数の問題」として捉えると、
対処法は自然と見えてきます。
-
比率が崩れているなら、
平らにする、再印刷する -
反射差が足りないなら、
光源や角度を変える -
計算で弾かれるなら、
手入力や別コードを使う
このように、
感覚的な対応ではなく、
論理的に次の手を選べる
ようになる点が、
数学で理解する最大のメリットです。
QRコードとの数学的違い
バーコードとQRコードは、どちらも情報を機械に伝えるためのコードですが、
数学的な考え方や情報の持ち方には大きな違いがあります。
この違いを理解すると、なぜ用途によって使い分けられているのかがはっきり見えてきます。
結論から言うと、バーコードは一次元の数学、
QRコードは二次元の数学を利用した仕組みだと考えると分かりやすいです。
バーコードは一次元、QRコードは二次元で情報を扱う
バーコードは、横方向に並んだ線と空白の連続によって情報を表現しています。
読み取り機は、一定方向にスキャンしながら、
線と空白の幅を数値として計測し、その並びを数列として処理します。
これは数学的に見ると、
一次元のデータ列を解析している状態です。
情報量は限られますが、その分、構造が単純で処理が速く、
多少の汚れや歪みがあっても安定して読み取れるという利点があります。
一方、QRコードは縦と横の両方向に情報を配置します。
黒と白のマス目を格子状に並べ、
それぞれの位置関係を含めて情報として扱います。
これは二次元配列のデータを解析している状態であり、
バーコードよりもはるかに多くの情報を格納できます。
誤り訂正の考え方の違い
数学的な違いが特に表れるのが、誤り訂正の仕組みです。
バーコードでは主にチェックデジットによって、
「正しいか・間違っているか」を判定します。
一方、QRコードでは、
誤り訂正符号と呼ばれる数学的手法が使われています。
一部が欠けたり汚れたりしても、
残りの情報から元の内容を復元できるように設計されています。
これは線形代数や符号理論に基づいた考え方で、
「間違いを検出する」だけでなく、
「間違いを修復する」ことまで視野に入れている点が、
バーコードとの大きな違いです。
用途によって使い分けられている理由
レジや物流の現場では、
高速で確実に読み取れることが最優先されます。
そのため、一次元で構造が単純なバーコードが今も主流です。
一方、URLや決済情報など、
多くの情報を一度に扱う必要がある場面では、
二次元で情報量の多いQRコードが適しています。
数学的な構造の違いが、
そのまま実用上の使い分けにつながっているのです。
なぜ手入力は危険なのか
バーコードが読み取れない場合、
数字を手入力すればいいと考える人も多いですが、
数学的に見ると、手入力は非常にリスクの高い行為です。
その理由は、人間の入力ミスが偶然にも
「正しい数値」に見えてしまう可能性があるからです。
人間の入力はランダム誤差が多い
人が数字を手入力する場合、
次のようなミスが頻繁に起こります。
- 数字の打ち間違い
- 桁の入れ替え
- 見間違いによる誤入力
これらは感覚的なミスであり、
本人が気づかないまま確定してしまうことも少なくありません。
チェックデジットがあるから「危険が見える」
JANコードなどのバーコードでは、
チェックデジットによって入力結果を計算で検証します。
そのため、手入力で1桁でも間違えると、
多くの場合はエラーとして弾かれます。
しかし、ここで重要なのは、
エラーになるのは「運が良いケース」だという点です。
まれに、誤入力した数字が偶然にも
チェックデジットの条件を満たしてしまうことがあります。
この場合、システム上は「正しい番号」として処理され、
間違った商品や情報が登録されてしまいます。
機械読み取りは数学的検証が前提
バーコード読み取りは、
線の幅、間隔、比率を数値として測定し、
その結果を数学的に検証します。
ここには人間の主観や感覚は入りません。
一方、手入力は人間の認知に依存します。
数学的な検証が最後に一度入るだけで、
途中過程はすべて感覚任せです。
この違いが積み重なることで、
手入力は「たまに大きな事故を起こす方法」になりやすいのです。
数学的に見た最適な対処法
バーコードが読み取れない場合は、
まず読み取り条件を整え、
機械による再スキャンを試みるのが最優先です。
どうしても手入力が必要な場合は、
複数人での確認や
元データとの突合を行い、
数学的検証を人為的に補う必要があります。
数学の視点で見ると、
「できるだけ人を介さない」
という設計思想こそが、
バーコードシステムの本質だと言えます。
まとめ|バーコードの仕組みは数学を知ると一気に分かりやすくなる
バーコードは、単なる黒と白の線の集まりではなく、
数学的なルールに基づいて設計された情報伝達手段です。
線の太さや間隔、並び方にはすべて意味があり、
それらは偶然ではなく、数として正確に扱われることを前提に作られています。
読み取り機は、バーコードを「模様」として見ているのではなく、
光の反射の変化を数値に変換し、
その数列を計算によって解析しています。
だからこそ、人の目では一瞬で判断できない情報でも、
高速かつ正確に読み取ることができるのです。
数学の視点で仕組みを理解すると、
バーコードがなぜ速く、なぜ読み間違えにくく、
そしてなぜ長年にわたって現場で使われ続けているのかが、
感覚ではなく理屈として見えてきます。
また、読み取れない原因や手入力の危険性といったトラブルも、
「印刷が悪いから」「機械の調子が悪いから」と曖昧に捉えるのではなく、
数や計算のズレとして説明できるようになります。
これは、日常や業務の中でバーコードを扱ううえで、
大きな安心感につながります。
身近すぎて意識することの少ないバーコードですが、
その裏側にはシンプルで合理的な数学の考え方が詰まっています。
少し視点を変えて仕組みを知るだけで、
普段何気なく見ているバーコードも、
「よくできた技術」として違った見え方をするはずです。


コメント